EN中文

地理研究 >

2022 , Vol. 41 >Issue 10: 2832 - 2850

DOI: https://doi.org/10.11821/dlyj020211075

研究论文

新疆地形复杂度的空间格局及地理特征

  • 张雪莹 , 1, 2 ,
  • 张正勇 , 1, 2 ,
  • 刘琳 1, 2 ,
  • 田浩 1, 2 ,
  • 康紫薇 1, 2 ,
  • 王统霞 1, 2 ,
  • 陈泓瑾 1, 2
展开
  • 1.石河子大学理学院,石河子 832000
  • 2.绿洲城镇与山盆系统生态兵团重点实验室,石河子 832000
张正勇（1978-）,男,甘肃景泰人,博士,教授,主要从事数字地形分析及水文水资源研究。E-mail:

张雪莹（1997-）,女,山东威海人,硕士,主要从事数字地形分析,GIS时空数据挖掘与分析研究。E-mail:

收稿日期: 2021-11-15

  录用日期: 2022-04-01

  网络出版日期: 2022-12-10

基金资助

国家自然科学基金项目(41761108)

第三次新疆综合科学考察项目(2021xjkk08)

收起

Spatial pattern and geographical characteristics of terrain complexity index in Xinjiang

  • ZHANG Xueying , 1, 2 ,
  • ZHANG Zhengyong , 1, 2 ,
  • LIU Lin 1, 2 ,
  • TIAN Hao 1, 2 ,
  • KANG Ziwei 1, 2 ,
  • WANG Tongxia 1, 2 ,
  • CHEN Hongjin 1, 2
Expand
  • 1. School of Science, Shihezi University, Shihezi 832000, China
  • 2. Xinjiang Production and Construction Corps Key Laboratory of Oasis Town and Mountain-basin System Ecology, Shihezi 832000, China

Received date: 2021-11-15

  Accepted date: 2022-04-01

  Online published: 2022-12-10

Fold

摘要

地形复杂度（TCI）是区域地表外在形态结构的数字化表达,既可表征坡面单元的多样性及其组合形式的复杂性,也可映射地球内外营力在地表留下“烙印”的过程,其客观描述和定量表达可为地表形态定义、刻画及分异等地形地貌理论研究提供重要依据。新疆独特的山盆地貌结构为地貌学研究提供了理想的场所。本文基于“倒金字塔滤网系统”逐步筛选微观和宏观坡面因子并确定权重进而构建地形复杂度模型;运用均值变点法确定新疆地形复杂度的最佳窗口,分析不同地貌单元地形复杂度的空间异质性,进一步探究不同营力作用对地表复杂程度的贡献。结果显示：① 地形复杂度模型综合相关性分析、聚类分析、变异系数法与主成分分析等方法对地形因子进行客观筛选与科学组合,使其具有全面客观性及独立有效性。② 地形复杂度以ASTER GDEM数据（30 m）为基础,得到最佳窗口（14×14）下全疆TCI介于0.13~46.36。山地与盆地相同地貌类型TCI面积占比峰值相近,不同地貌类型可比较其斜率、偏度及峰度得以区分。在经纬向上能更好的刻画出独立山峰及深切峡谷等局部地形分异,TCI≈1可作为平原与山地地貌单元之间的分界值。在高程分区下TCI>2时为各山系（山群）震荡高程区起始处,山麓处TCI曲线差异显著。③ 地形复杂度能较好的体现不同外营力在地表留下的痕迹,一定程度上也可表征外营力对不同成因地貌类型的贡献度。本研究对新疆地形地貌的形态特征和形成原因等方面提供理论依据和科学方法,可为地形地貌研究、生态环境影响以及区域发展评价提供实践指导。

关键词： 地形复杂度; 坡面因子; 最佳窗口; 地理特征

本文引用格式

张雪莹 , 张正勇 , 刘琳 , 田浩 , 康紫薇 , 王统霞 , 陈泓瑾 . 新疆地形复杂度的空间格局及地理特征[J]. 地理研究, 2022 , 41(10) : 2832 -2850 . DOI: 10.11821/dlyj020211075

Abstract

Terrain Complexity index (TCI) is a digital representation of the external morphological structure of the regional surface. The TCI can characterize the diversity of slope units and the complexity of their combination forms, and also map the process of "imprinting" the Earth's internal and external forces on the surface. The objective description and quantitative expression of TCI can provide an important basis for topographic and geomorphological theoretical studies such as definition, characterization, and differentiation of surface morphology. The unique mountain-basin geomorphic structure in Xinjiang provides an ideal place for geomorphological research. This paper is based on the "inverted pyramid filter system" to gradually filter micro and macro slope factors and determine the weights to build a TCI model. The mean change point method was used to determine the optimal window of TCI in Xinjiang, analyze the spatial heterogeneity of TCI of different geomorphic units, and further explore the contribution of different forces to TCI. The results show that: (1) The TCI model is objectively screened and scientifically combined with correlation analysis, cluster analysis, coefficient of variation method, and principal component analysis so that the TCI model has overall objectivity and independent validity. (2) The TCI is based on the global Digital Elevation Model (ASTER GDEM, 30 m) terrain data (V2), and the TCI of the whole of Xinjiang is between 0.13 and 46.36 under the optimal window (14×14). The peak value of the TCI area of the same geomorphic type is similar to that of the basin, and the slope, skewness, and kurtosis of different geomorphic types can be compared to distinguish them. Local topographic differentiation, such as independent peaks and deep canyons, can be better characterized in longitude and latitude, and TCI equal to about 1 can be used as the boundary value between plain and mountain geomorphic units. When TCI is greater than 2 in elevation division, it is the beginning of the oscillation elevation region of each mountain system (mountain group), and the TCI curves at the foothills are significantly different. (3) TCI can better reflect the traces left by different exogenous forces on the surface, and to a certain extent, it can also represent the contribution of exogenous forces to different genetic geomorphic types. This study provides the theoretical basis and scientific method for the formation reasons and morphological characteristics of topography and geomorphology in Xinjiang and provides practical guidance for topography and geomorphology research, ecological environment impact, and regional development evaluation.

Key words： terrain complexity index; slope factor; optimal window; geographic features

1 引言

地形复杂度（Terrain complexity index,TCI）是描述地表形态和变化程度的重要参数[1]。它既可以表达宏观尺度地貌单元的整体相似性,也可刻画微观尺度地表的不规则性[2⇓-4]。TCI相关研究不仅有益于传统地形地貌学理论的拓展和深入[5⇓⇓⇓⇓-10],同时在规划布局选址[11,12]、资源环境适宜性评价[13,14]、局地气候变化研究[15⇓-17]等领域也具有重要参考价值。为了科学地认识和分析地貌特征,学者们依地貌成因、形态和物质构成等相对一致的空间单元将地表划分为不同地貌单元,这虽有利于大尺度地表形态特征的研究,但局限了对地貌单元内部形态差异性分析。地形起伏度、坡度/坡向及地形切割深度等地形指标可从不同角度细致刻画局部地表形态特征,其中地形起伏度[18]多以某确定面积内最高点与最低点的高差表达地表形态差异性,坡度和坡向[19]描述局部地表在空间的倾斜程度和倾斜方向,地形切割深度[20]可反映地表的侵蚀深切程度等,以上地形指标的表达各有侧重但对区域地表形态复杂程度的综合表达不够全面[1]。汤国安等指出,地球表面由不同坡面组合而成,坡度、坡向、坡长等几何特征构成了坡面的多重属性,不同坡面的组合形式（即坡面复合体）造就了地表形态复杂程度各异[21]141。因此,构建以坡面为基本单元且综合反映微观/宏观坡面组合的地形复杂度指标体系,可实现对地表形态异质性的精细描述和全面表征。
当前地形复杂度的表征或定量表达主要包括几何分析法和统计分析法。前者是对地貌单元几何形态的描述,如利用相邻坡面的夹角大小变化反映地形差异[22]、运用栅格法向量计算空间夹角[23]、结合元分维模型理论[3,4]以及分维值[24]表征地形复杂度。此方法评价结果精度虽高,但存在算法复杂和缺乏普适性等不足之处,限制了其在大尺度区域的应用和推广。统计分析法则在选取多种地形因子的基础上,运用数理统计方法进行多因子组合表达,算法简易且具有广泛适用性,但依赖于地形因子的客观选取和数据分析方法的科学选择。地形复杂度相关的地形因子之间往往存在不同程度的信息重叠,需进行剔除以避免指标选取的主观性。为此,依据地形因子的关系特征和计量特征,并基于全面客观性和独立有效性等原则对地形因子进行筛选,可使地形复杂度指标的构建更为科学。
“尺度”无处不在,适宜的空间尺度是地学研究中一个关键的参数,正如地理学中的尺度效应认为：“在不同观察尺度上,往往会得到不同的观测结果”[25]。统计单元面积不同所反映区域地表形态的局部和整体复杂程度各异[26]。界定窗口尺度常用的方法有最大高差法、最大高差-面积比法、人工作图法、均值变点法等[26,27],其中均值变点法运用最为广泛且更加客观[28⇓-30]。
地貌系统是一个统一整体的动力系统。地球表面在内外营力的长期作用下不断演化形成不同地貌形态[31]。内营力作用形成地表基本起伏形态与空间格局,外营力则对地表进行剥蚀塑造和削高填低,改变地表复杂程度[32]。外营力塑造地貌包括侵蚀和堆积两大过程,二者相辅相成,既反映出地貌营力的强度及对区域地形复杂度的能量贡献,又映射着区域地貌的形成机制与演化规律。新疆地貌类型丰富,拥有除海成地貌类型外几乎所有不同成因的地貌类型,其独特的山盆地貌结构特征更为地貌学研究提供了理想的场所[33]。本文选取新疆典型地貌样区,以坡面为单元,基于全球数字高程模型数据,采用“倒金字塔滤网系统”模式,结合相关性分析、聚类分析、变异系数以及主成分分析等方法逐层遴选地形特征因子确定权重,进而构建地形复杂度模型,并运用均值变点法计算新疆地形复杂度的最佳窗口,实现地形复杂度对区域地表形态的有效表征;在此基础上进一步分析不同地貌单元及空间尺度下地形复杂度的分异规律,探究不同外营力对区域地表形态复杂性的作用强度,以期为地形地貌理论及应用研究、生态环境保护以及区域发展影响评价等提供理论依据与技术支持。

2 研究方法与数据来源

2.1 数据来源

本研究主要采用数字高程模型（ASTER GDEM）和数字地貌数据,其中GDEM（30 m×30 m）数据在山区和平原区精度均较高[34],用于提取高程带分区及计算各类地形因子,为构建地形复杂度模型提供基础数据,来源于地理空间数据云（ http://www.gscloud.cn）;地貌类数据采用中国西部1 ∶100万数字地貌数据集,包括25种基本地貌类型以及10种成因类型[35],体现了不同营力作用下形成的地貌类型、成因及其空间分布,来源于国家冰川冻土沙漠科学数据中心（ http://www.ncdc.ac.cn）。

2.2 地形复杂度模型的构建原理

本研究基于开放式“倒金字塔滤网系统”模式构建地形复杂度模型（图1）。首先广泛选取与地表形态有关的地形因子,参考以往学者的分类标准并考虑数据可得性,构建客观全面的地形复杂度指标体系;然后运用相关性分析法剔除指标无关项和信息冗余项,聚类分析法进行有效归并,采用变异系数法识别最大贡献因子,即可优选有效且独立的指标;最后利用主成分分析法进行线性变换确定各因子权重,进而完成地形复杂度模型构建。
图1 优选地形复杂度指标的倒金字塔滤网模式

Fig. 1 Optimization of terrain complexity index (TCI) inverted pyramid filter model

2.2.1 地形复杂度的指标选取原则

影响地形复杂度的指标因素众多,为科学表征地形的复杂程度,筛选地形因子需要遵循客观有效的原则依据。综合以往学者在表征不同尺度地表形态指标因子的选取经验[1,7,36⇓-38],并结合地表由诸多连续坡面以不同形式组合而成的现实情况,本研究拟遵循全面客观性和独立有效性两大原则构建复杂度指标体系,其中全面客观性是海选因子的第一原则,全面选取描述地形空间分异的地形因子,并考虑地表基本形态和地貌特征因子客观性;独立有效性是评价因子的最重要原则,为保证选取的地形因子符合研究目的且具有代表性和独立性,防止各地形因子高度相关从而产生信息重叠和冗余,确保复杂度的计算过程和结果。

2.2.2 地形复杂度的指标体系构建

地形复杂度指标用于刻画不同地形特征和空间分布,不同学者根据地形因子的应用场景和空间对其进行分类。Wilson根据因子是否直接由高程数据得出,将地形因子分为单因子属性和复合属性[39];Florinsky按照计算特性划分局部地形因子和非局部地形因子[40],以上的因子区分和归并均未考虑到地表过程发生发展的基本单元即坡面。汤国安描述地球表面是由不同坡面构成,微观坡面因子可反映该地貌在小尺度地表单元的形态、起伏或扭曲等特征,而宏观坡面因子能反映大尺度下地貌的总体形态特征[21]142。以坡面为基本单元划分地形因子有助于从不同尺度描述地表坡面形态的细部复杂性和地貌单元的整体连续性。故本研究根据坡面因子的关系特征和计量特征,结合全面客观性和独立有效性原则,由坡面姿态因子、坡面曲率因子、坡形因子、坡长因子等共同表达坡面的微观特征,坡面异质性因子、坡面复合因子等反映坡面的宏观特征（表1）。
表1 地形复杂度因子分类及描述

Tab. 1 Classification and description of terrain complexity index (TCI)

尺度 坡面因子 具体指标 符号 量纲 描述与表达
微观 坡面姿态因子 坡度 SLO ° 局部地表倾斜程度,即坡角的正切值
坡向 ASP ° 坡面法线在水平面的投影方向
坡度变率 SOS - 坡度的变化率,即坡度的坡度
坡向变率 SOA - 坡向的变化率,即坡向的坡度
坡面曲率因子 全曲率 CUR m - 1 刻画曲面整体性质的曲率
剖面曲率 PRC m - 1 刻画曲面在水平方向上的变化
平面曲率 PLC m - 1 刻画曲面在垂直方向上的高程变化率
坡形因子 坡形 SF - 各种不同坡面的几何形态
坡长因子 坡长 SL m 地面一点到其水流起点的最大距离在水平方向的投影长度
宏观 坡面异质性因子 地形起伏度 RDLS m 领域范围内所有栅格中最大与最小高程之差
地形粗糙度 TR - 地表实际面积与投影面积的比值
地形切割深度 TCD m 领域范围内平均高程与最小高程的差值
高程变异系数 EVO - 领域范围内高程标准差与平均值的比值
坡面复合因子 地形位指数 TPI - 高程和坡度组合而成
其中大部分指标的计算参考常规公式[41],并对部分特殊因子的计算方式进行优化,计算方法分别如下：坡面姿态因子下坡度采用三阶不带权差分法以提高不同地形区的适用性[42];坡向变率运用反地形法[43]进行校正。尤其要指出,以往的坡长仅考虑水流起点间最大距离的投影长度,而孔亚平等构建的土壤侵蚀模型[44]在一定程度上可反映土壤侵蚀外营力对地形复杂度的影响。为此采用以下公式（1）计算坡长因子指数m。
m = β / ( β + 1 )
式中： β = ( s i n θ / 0.0896 ) / ( 3.0 s i n θ 0.8 + 0.56 );θ为坡度（°）。
地形位指数将高程和坡度进行组合,可综合反映地形的空间分异特征[45]。高程与坡度同时出现高值时地形位较大,反之则地形位较小,其公式如下：
T P I = l o g E E - + 1 × S S - + 1
式中：TPI为地形位;E及 E -分别代表高程值和该窗口下平均高程值;S与 S -分别代表坡度值和该窗口下平均坡度值。

2.3 最佳统计窗口确定

“尺度”问题是地形复杂度客观表达的必然需要,随着分析窗口增大,复杂度随窗口面积的变化呈logarithmic曲线[46]。该曲线上必定有且仅有一个拐点使图像由陡变缓,该点所对应的窗口值即为所求最佳统计单元[28]。本文采用均值变点分析法[26⇓⇓⇓-30]确定地形复杂度的最佳窗口。

3 结果分析

3.1 地形复杂度模型构建实证

3.1.1 典型地貌样区的选取

为提取地形复杂度模型构建所需的各类坡面指标因子,选取贯穿新疆南、北最远点相连的剖面线,其可涵盖研究区的山地、盆地和平原等地形地貌类型（图2）。在剖面线所经区域选取九类典型地貌单元,具体如下：① 山顶：低海拔山顶、中海拔山顶、高海拔山顶;② 山脊;③ 山谷：峡谷、河流谷地、河流阶地;④ 鞍部;⑤ 陡崖;⑥ 平原：冲击平原、山间平原、高海拔平原;⑦ 丘陵：山前丘陵、高海拔丘陵;⑧ 沙丘;⑨ 沙垄。为保证以上样区对典型地貌局部特征的表现性以及数据总量的易于计算性,多次尝试后将每个样区的边长设定为3 km,每个样区产生10000个指标样本数据,为地形复杂度指标的筛选和确定提供基础。
图2 研究区剖面线及典型地貌样区

注：基于自然资源部国家基础地理信息中心全国地理信息资源目录服务系统的标准地图（审图号：GS(2016)2556号）绘制,底图无修改。

Fig. 2 Section line and typical geomorphic area of the study area

3.1.2 地形复杂度的指标因子筛选

坡面因子分布呈无序性,因子间亦存在不同程度的相关性[47]。考虑到ASP因子的数据类型,以及参考前人的研究成果[1,48],首先在初选阶段将其进行剔除。为了保证复杂度指标的独立性,避免指标信息重叠和数据冗余,需对坡面因子进行筛选。Spearman秩相关系数法对原始数据分布无要求,可用于剔除无关指标（图3a）;结合聚类分析法将具有相似特征的变量归为一类,并结合变异系数法进一步优选因子。从图3a可以看出各因子之间都具有一定的相关性,坡面异质性因子下的指标表现出极强的正相关,坡面曲率因子下全曲率与平面曲率呈正相关,而剖面曲率与两者呈负相关。坡面姿态因子与坡面异质性因子呈负相关且数值较高。聚类分析后可将14种坡面因子归并为六类（图3b）。
图3 地形因子相关性分析及聚类分析图

注：地形因子符号含义详见表1。

Fig. 3 Correlation analysis and cluster analysis of terrain factors

对于聚类归并后具有相似性的各类指标,须进一步遴选每类中最重要的指标并舍弃影响力小的指标,进而确定地形复杂度核心指标。变异系数法可实现聚类指标的因子优选,通过变异系数筛选出同一类别中信息含量最大且对地形复杂度影响最为显著的核心指标（表2）。变异系数的计算公式为[7]：
C V j = 1 n ∑ i = 1 n x i j - x j ¯ x j ¯
x j ¯ = 1 n ∑ i = 1 n x i j
式中： C V j是第j个地形特征因子指标的变异系数;n为样本个数; x i j为第j个指标的第i个样本值; x j ¯为第j个指标的n个样本均值。
表2 变异系数及筛选结果

Tab. 2 Coefficient of variation and screening results

地形因子 变异系数值 是否选用
SF 1.202 √
CUR 1.108 ×
PLC 1.100 ×
TPI 0.104 √
EVO 0.866 ×
SLO 0.367 ×
TR 0.813 ×
RDLS 0.914 √
TCD 0.894 ×
SOS 0.158 ×
SOA 0.412 √
SL 3.467 √
PRC 1.128 √

注：地形因子符号含义详见表1。

运用相关系数法剔除无关项、聚类分析进行有效归并以及变异系数法识别最大贡献因子进行综合筛选,最终确定6个核心指标用以构建地形复杂度模型,分别为：地形位指数（TPI）,地形起伏度（RDLS）,坡形（SF）,坡向变率（SOA）,坡长（SL）,剖面曲率（PRC）。

3.1.3 复杂度经验模型构建

地表形态的复杂程度是由各坡面因子数值差异及其组合方式等共同决定的。模型构建时需探知核心指标对地形复杂度表征的贡献程度。本研究采用主成分分析法[49]确定各因子的客观权重,运用均值标准化方法对原始核心指标数据进行无量纲化处理,并基于协方差矩阵得到主成分解释方差和载荷矩阵。结果显示前两个主成分累积贡献率可达95.52%,可较好概括核心因子的主要信息。基于载荷矩阵和特征值计算主成分的系数值,再带入公式（5）得到综合系数值。
T C I j = ∑ i = 1 n a i j × C R i ∑ i = 1 n C R i
式中： T C I j为指标j的综合系数;n为保留的主成分个数; C R i为第i个主成分贡献率; a i j为指标j在第i个主成分中的系数值。
对标准化后的地形复杂度关系系数进行归一化得到如下公式：
T C I s = 0.2465 T P I S + 0.3261 R D L S S + 0.2117 S F S + 0.0127 S O A S + 0.0794 S L S + 0.1236 P R C S
式中：下标s表示为指标均值标准化值。
反标准化处理可直接反映TCI与原始地形因子的对应关系,得到便于计算的地形复杂度模型：
T C I = 0.4153 T P I + 0.0177 R D L S + 0.0425 S F + 0.0003 S O A + 0.1487 S L + 0.2151 P R C

3.2 新疆地形复杂度的最佳窗口

地形复杂度刻画地表形态特征时对尺度有较强的依赖性,分析窗口的大小决定区域地势复杂程度的表达形式。采用均值变点法计算不同窗口面积下地形复杂度,判断统计学意义下的最佳空间尺度。TCI所对应的S-Sk值,前后曲线走势由骤增变减缓,其中最大值对应的突变点即为最佳窗口。由图4可见新疆地形复杂度最佳窗口面积为 17.64 × 10 4m2（14 ×14,矩形邻域）。
图4 不同窗口面积下S-Sk的变化范围图

Fig. 4 Scatter diagram of S-Sk variation range under different window areas

基于数理统计得出的最佳窗口面积有必要进一步判断其在地貌学视角下的尺度效应,为此随机选取高海拔山地、沙垄以及冲积平原三种地貌样区,比较3×3、14×14和30×30三种分析窗口下TCI对地形地貌的表达和识别效果。由表3可以看出：3×3窗口下TCI突出数据细碎部表达,但同时“噪声”干扰较多,地貌形态的整体性和连续性亦被淹没;30×30窗口下数据平滑且概化严重,难以呈现地形的碎部特征和地表形态的异质性;而14×14窗口下的TCI则兼顾地形的碎部细节和地貌整体连续性,如高海拔山地样区内的山顶区和河谷地段均较完整且连续保留;沙垄脊线清晰可见,易于识别沙丘的迎风坡和背风坡等地形特征;冲积平原区湖泊/水库边界线更加自然平滑,河流出山口处亦能较好的刻画出河道的冲刷和切割痕迹。由此可见,分析窗口较小虽利于刻画微观地形特征,但无法反映大尺度地貌格局,“损坏”了地貌单元的完整性和独立性;分析窗口较大有利于涵盖更完整的地貌区,但“模糊”了典型地貌单元内部的差异性。新疆地形复杂度 17.64 × 10 4m2（14 ×14）矩形邻域,不仅是统计学意义下的最佳窗口,也是对典型地貌特征具有清晰指示性的地理学最佳窗口。
表3 不同窗口下三种地貌样区的地形复杂度效果对比

Tab.3 Horizontal comparison of terrain complexity index (TCI) in different windows of the three geomorphic types

3.3 新疆地形复杂度的空间分布特征

新疆地形复杂度由高海拔山区向低海拔平原和盆地递减（图5）。在最佳窗口下TCI均值为1.00,对应土地面积占比呈正态分布趋势且分界点明显。其值为0.7处相应土地面积占比最大（21.84%）,TCI介于0.5~2.0区间的土地占总面积达91.01%。最大值位于喀喇昆仑山主峰乔戈里峰（K2）,峰顶平均海拔与相对高差分别高达8611 m和2842 m,最小值分布于湖泊/水库区。新疆南北部平原及盆地外围地区的TCI大多小于0.7,阿尔泰山南部、天山外围区、以及南部的帕米尔高原、喀喇昆仑山、昆仑山和阿尔金山等山系（简称帕喀昆阿山群）东南部和各盆地中央沙丘区的TCI在0.7~1.5之间。中高、高海拔山区TCI增大至1.6~4。TCI大于4的区域土地面积占总面积小于0.01%,零星分布在天山布罗克努山脉、帕米尔高原及喀喇昆仑山极高海拔地区。整体来看,研究区地形复杂度空间分布依山-盆整体地貌格局呈环形分布,与海拔呈较强正向对应关系。
图5 新疆地形复杂度空间分布及土地面积占比

注：基于自然资源部国家基础地理信息中心全国地理信息资源目录服务系统的标准地图（审图号：GS(2016)2556号）绘制,底图无修改。

Fig. 5 Spatial distribution of terrain complexity index (TCI) and land area change in Xinjiang

3.3.1 新疆不同地貌单元地形复杂度的空间分布

新疆山-盆相间的分布格局使得各地貌单元地形的整体复杂程度具有明显的差异性。山区（山群）和盆地的复杂度面积占比呈近似正态分布趋势（图6）。按各地貌单元的TCI面积占比峰值排序为：阿尔泰山（1.3）>帕喀昆阿山群（1.0）>天山（0.8）>塔里木盆地（0.7）=吐哈盆地（0.7）=准噶尔盆地（0.7）。相同地貌类型的地形复杂度面积占比峰值较为接近,其中阿尔泰山最大,帕喀昆阿山群次之,而天山最小,是由于帕喀昆阿山群东南部和西部为大面积高海拔平原及山间盆地,天山东部和南部拥有大面积山前平原区,而阿尔泰山较少分布以上地形,可能是由于未统计蒙古国境内的高原所致。山区在TCI区间1~2中面积占比出现“阶地”式变化,此处可能为中海拔山峰密集处。而盆地则呈正态分布趋势,TCI面积占比峰值均为0.7,集中分布在准噶尔与吐哈盆地外围地区,而塔里木盆地呈双环状分布,边缘则是与山地连接的砾石戈壁及冲积平原,中心分布形态各异的沙丘和沙垄地形复杂度值较高。从TCI的分布范围和面积占比的曲线走势来看,山区主要分布在TCI区间0.5~2.5,较为容易区分出阿尔泰山。由于其曲线斜率值在TCI区间1~2时相对较小（0.065）,且在TCI>2时面积占比较小,可反映出阿尔泰山相较于天山（0.079）和帕喀昆阿山群（0.081）山体规模较小起伏平缓。而盆地主要分布范围为0.3~1.2,虽各盆地总面积大小相差较大,但面积分布曲线的走势高度相似,仅峰度和偏度略有差别,吐哈（8.68）及塔里木盆地（8.64）较准噶尔盆地（2.30）峰度更大,其原因为吐哈及塔里木盆地山前带多发育为“推覆型”构造,地表条件更为复杂[50]。总体来看,新疆山区（山群）和盆地可从地形复杂度对应面积占比及累计百分比曲线的走势得以区分,有助于标识和区分地表形态的整体差异性和内部相似性。
图6 不同地貌单元地形复杂度的面积变化及累积百分比图

Fig. 6 Area variation and cumulative percentage of terrain complexity index (TCI) of different geomorphic units

3.3.2 新疆地形复杂度的经纬向分布特征

为进一步探究新疆地形复杂度与局部微地形特征的对应关系,分别沿纬向（37°N、39°N、43°N、45°N）（图7a~图7d）和经向（83°E、85°E、87°E、89°E）（图7e~图7h）分析多种典型地貌类型地形复杂度与海拔的对应关系（R=0.582）。
图7 新疆地形复杂度纬向、经向分布规律

Fig. 7 The latitudinal and longitudinal distribution features of the terrain complexity index (TCI) in Xinjiang, China

纬向剖面线能横穿多种典型地貌类型。37°N一线地形复杂度变化剧烈,TCI介于0.33~4.32（均值1.24）,分别于克勒古拉木山东南处（77.6°E）、于田县塔里木沙漠南缘（82.2°E）处出现最大值和最小值。塔里木盆地与库木库勒盆地TCI值域接近但海拔相差较大,后者是位于昆仑山腹地的高原盆地,TCI变化较塔里木盆地南部冲积平原更为剧烈。海拔相同的两点（图7a中a1、a2）均位于山间谷地,但TCI略有差异分别为0.66和1.13。39°N一线TCI介于0.39~3.01（均值0.89）,在萨雷阔勒岭向木吉谷地过渡区域（74.4~74.6°E）出现大幅下降,高差可达889 m。塔里木盆地腹地的沙丘和沙垄（图7b中b1、b2）使得局部区域复杂度突出,TCI最高可达1.66和1.62。43°N一线TCI介于0.38~5.18（均值1.02）变化剧烈且在87.9°E处（天山托克逊红河谷断崖边）达到最大值。TCI对独立山峰具有较好刻画（图7c中c1、c2）,可识别出连续海拔下微小起伏的山地。45°N一线TCI介于0.38~2.96（均值0.85）,东西向变化相对平缓呈近“U”型分布。阿拉套山（图7d中d1）相较于北塔山（图7d中d2）海拔更高,但复杂度却较小,可见并非海拔越高复杂度越大,TCI可有助于识别出海拔较低处更为复杂的区域。
经线纵穿新疆山-盆相间的各类地貌单元。83°E一线TCI介于0.13~3.02（均值0.99）,于相对开阔平坦的伊犁河谷（43.5°N）、额敏河谷（44.9°N）和塔额盆地（46.5°N）处出现明显低值。昆仑山一带（35.5~37°N）海拔浮动较小均在5000 m以上,TCI可识别出高海拔平原（图7e中e1,TCI=1.13）与山地（图7e中e2,TCI=2.86）之间的差异。85°E一线TCI介于0.43~10.11（均值0.98）,峰值出现在哈尔阿特河谷（43.8°N）,其海拔（2243 m）远低于周边区域,在流水侵蚀和冲刷作用下形成了深切的“V”型谷区。山谷地形TCI（图7f中f2,TCI=1.05）明显大于河谷地形（图7f中f1,TCI=0.68）。87°E和89°E纵穿地貌相近,TCI分别为0.39~3.10（均值0.98）与0.47~2.94（均值0.92）,TCI87°E较TCI89°E更大,在库鲁克塔格山脉、博斯腾湖以及天山中段变化非常剧烈。选取山区和盆地以及山麓处TCI相对较高的特殊点进行比较,山腰处（图7g中g1、g2）海拔较低但相邻地形起伏较大,故TCI（2.61,1.95）较高。塔里木盆地处深切的干涸河道（图7h中h1）以及博格达峰山麓处的松散沉积物（图7g中h2）使得TCI异常增高。
整体来看,新疆地表形态呈东西两端复杂而中部相对简单,南北空间变化与山-盆呈阶梯式错落分布高度吻合,与剖面线所经地貌类型高度一致。TCI对局部地形分异具有较好的指示性,其突变点可表征出独立山峰、深切峡谷以及盆地内部沙丘和沙垄等局部特征地形,同时也可辅助识别地貌单元的位置和边界,如TCI≈1可作为平原与山地之间的分界值,TCI>2可视为高海拔和极高海拔山区的分布范围。此外,TCI与海拔变化趋势基本一致,但可进一步识别出相同海拔下地形更为复杂的地貌单元,例如昆仑山南部山前平原海拔较高,无法仅从高程反映山体所在位置,故而结合地形复杂度可更细致地刻画出地形地貌的分布及形态。

3.3.3 新疆地形复杂度的海拔分区

区域内高程变化直接影响地表形态复杂程度,反映了区域地貌形成的总能量水平[51]。通过全疆及区内三大山系（山群）不同高程分区TCI均值的空间统计分析可知（图8）。TCI随海拔升高而增加,但存在显著的高程分异。除阿尔泰山外,TCI在低海拔区域均呈小幅平缓增加,而出现强烈震荡的高程区间则差异显著。全疆TCI震荡区间为6000~7700 m,且在海拔1700~5000 m呈缓慢上升趋势,该高程区间大多为山峰错落和密布区,也是全疆中高海拔山区分布所致。由北至南三大山区TCI均值震荡所对应的海拔区间依次增大,其中北部的阿尔泰山山体规模较小,分布在900~1000 m和3200~4000 m均出现大幅震荡。海拔1000 m以下TCI均值出现高值区,最大值可达2.38,但在海拔1000 m处出现了骤降,均值仅0.70。海拔1000 m以上TCI均值平缓上升,在3687 m处（哈巴河河口）达到峰值3.79。中部的天山及南部的帕喀昆阿山群TCI均值整体变化趋势相似,但天山TCI均值震荡高程区最宽,在4300~7200 m震荡幅度明显。而帕喀昆阿山群TCI均值震荡高程区仅在6400~7700 m,且在喀喇昆仑山（7166 m）处达到最大值22.48。总而言之,TCI>2时可视为各山系（山群）震荡高程区起始处。另外发现,各山区山麓处（图中放大区域）TCI均值曲线呈较明显起伏特征,阿尔泰山和天山的曲线波动剧烈且TCI均值较高,是由于新疆北部山区水资源较丰富,山麓处广布流水切割形成山谷或峡谷[52],使得复杂度值高于帕喀昆阿山群北部山麓。整体来看,高程变化在宏观上与地形复杂度均值变化呈正向对应关系,但区域内山峰、河谷和峡谷的分布共同影响地形复杂度空间分异,进一步表明地形复杂度指标是对以往仅靠高程变化划分地貌单元的有益补充。
图8 新疆典型山区地形复杂度空间分布

注：图中图表示箭头所指区间的变化。

Fig. 8 Average distribution of terrain complexity index (TCI) in typical mountainous areas and the whole Xinjiang

4 讨论

在地球内外营力长期共同作用下,地表起伏不断发生变化,形成不同复杂程度的地貌形态[53]。其中外营力对地表进行剥蚀塑造和削高填低改变了地表复杂程度[32]。依据外营力成因划分为：湖成地貌、流水地貌、冰川地貌、冰缘地貌、风成地貌及干燥地貌等;依据特殊物质属性划分为：黄土地貌、喀斯特地貌以及花岗岩地貌等[54]。新疆地处中国西北干旱区,拥有除海成地貌外几乎所有地貌类型,该区域地貌外营力作用可归纳为堆积和侵蚀两大类,主要表现为风力和流水的搬运和侵蚀、冰川运动剥蚀和寒冻机械风化等作用进而控制地表形态。以上各外营力的作用区域和尺度不尽相同,同时在不同属性物质（如黄土和花岗岩等）组成的地貌单元表面留下形态各异的“烙印”。为此,本文尝试探究外营力对新疆地表形态复杂度的贡献和影响程度。
经分区统计新疆不同地貌类型下（平原、台地、丘陵和山地）地形复杂度的面积占比,及各海拔区间对应地形复杂度的分布特征（图9）,发现不同成因地貌类型的分布具有一定的空间差异性,各外营力对地表的堆积和侵蚀等作用强度各异。流水地貌和湖成地貌主要基于水体的流动性对地球表面侵蚀和冲积以及汇聚成湖泊之后对湖岸的冲刷和堆积,但TCI的分布范围差异较大,湖成侵蚀作用下TCI最大值（1.19）仅出现于低海拔台地,流水侵蚀作用最大值（25.20）位于中海拔山地。地处山地与盆地过渡带的中海拔平原（占比6.34%）受流水堆积作用影响最大,而湖成堆积主要作用于由湖积平原和低阶地组成低海拔平原（占比1.06%）,如塔里木盆地东部罗布泊处。冰川与冰缘地貌整体TCI分布范围相近,且集中分布在中高和极高海拔山区,冰缘地貌TCI（0.34~18.75）大多小于相同地形和海拔下的冰川地貌TCI（0.32~33.15）,是由于冰川地貌在冰川运动剥蚀作用下,外形棱角分明且存在于山脊和冰川槽谷[55],而冰缘地貌在冻融和雪融过程的主导外营力下使得地表被夷平,其主要分布在地形较为平缓的山坡区。新疆地貌成因类型中风成和干燥作用占主导地位,这两种类型的地貌占全疆总面积的51.27%。风成地貌发生风积可使流沙扩展,而风蚀则形成洼地和残丘。研究区风成地貌主要以风积作用下的中低海拔丘陵（沙丘）为主,其TCI范围为0.13~3.30,面积占比为15.96%。而干燥地貌TCI均值（0.86）略大于风成地貌（0.74）,因该地貌类型主要为干燥剥蚀平原以及干燥作用的丘陵和山地,大多分布在准噶尔盆地和塔里木盆地外围与山地相连的砾石戈壁。总体来看,TCI可对堆积或侵蚀作用类型及地貌成因类型进行辅助判读。堆积作用形成的地貌区的TCI相对较低,其均值在平原和台地处均小于1,即便是丘陵和山地TCI均值最高不超过1.2,而侵蚀作用下例如流水侵蚀或冰川侵蚀作用,TCI均值最高可达1.9,因此可结合TCI进行辅助判别堆积和侵蚀等外力作用类型;TCI阈值在一定程度上可以识别地貌成因类型,如在流水作用下TCI可达20以上,而湖成作用TCI小于4。干燥作用下TCI可高达25以上,而风成堆积作用TCI最高仅为3.91。因此结合堆积和侵蚀对新疆地貌形态作用区域和强度的差异性,地形复杂度指标可作为地貌成因类型判别的依据。
图9 新疆典型地貌成因地形复杂度分布范围及面积占比图

Fig. 9 Distribution range and area proportion of terrain complexity index (TCI) of typical landforms in Xinjiang

另外,地貌物质组成是控制地貌形成与发育的关键因子之一,外营力与不同属性结构（紧实、松散等）物质的作用效果关系密切[56]。新疆拥有四种特殊物质组成控制的地貌类型（图10）。其中,黄土地貌堆积作用仅出现在中低海拔平原地区（均值：0.77）,其TCI（0.13~4.74）较小,主要呈条带状分布在天山北麓及昆仑山西部,黄土结构松散使该地貌形态呈沟壑众多且较为破碎,塑造其地表的外动力类型较多,其中风力作用具有既可搬运堆积又可吹蚀吹扬的夷平效果;喀斯特地貌零星分布在昆仑山东部鲸鱼湖以西和阿共克勒湖以南的高海拔及极高海拔山区,TCI均值可达1.73。而花岗岩侵蚀作用面积占比曲线呈波形浮动,在中海拔台地处出现峰值（0.30%）,喀斯特地貌是经水流对可溶性岩石的侵蚀和溶蚀而形成,而坚硬的花岗岩地貌通过强烈的风蚀及流水切割可形成奇峰深壑,两种地貌都常见于山区且仅存在侵蚀过程;内外营力共同作用下的火山熔岩地貌TCI范围可达0.63~2.43,分布于新疆于田县极高海拔山区阿什库勒火山处,是新疆最大的火山群。整体来看特殊物质组成控制的地貌类型受侵蚀作用的面积占比较大,其中喀斯特和火山熔岩侵蚀作用主要分布在台地、丘陵和山地中高海拔处,而黄土和花岗岩地貌在各个海拔下均有分布。四种特殊物质组成控制的地貌类型仅占新疆总面积的3.69%,还需在其他地区进行进一步验证。总体而言,地形复杂度能较好的体现不同外营力对地表留下的痕迹,一定程度上也可表征内外营力对不同成因地貌类型的贡献度。
图10 新疆典型地貌成因地形复杂度分布范围及面积占比图

Fig. 10 Distribution range and area proportion of terrain complexity index (TCI) of typical landforms in Xinjiang

5 结论

（1）基于开放式“倒金字塔滤网系统”构建地形复杂度模型,并得出地形复杂度与地形位指数（TPI）、地形起伏度（RDLS）、坡形（SF）、坡向变率（SOA）、坡长（SL）以及剖面曲率因子（PRC）之间构建的经验公式 C = 0.4153 T P I + 0.0177 R D L S + 0.0425 S F + 0.0003 S O A + 0.1487 S L + 0.2151 P R C。
（2）地形复杂度以ASTER GDEM数据（30 m）为基础,得到最佳窗口（14 ×14）通过统计学和地理学意义下的双重验证,新疆TCI介于0.13~46.36,TCI呈现环形分布且与海拔呈正向对应关系;山地与盆地相同地貌类型TCI的面积占比峰值相近,不同地貌类型可从TCI面积占比的曲线走势的斜率、偏度和峰度得以区分。TCI在经纬向上对局部地形分异也具有较好的指示性,其突变点可以很好的表征出独立山峰、深切峡谷以及盆地内部沙丘和沙垄等局部特征地形,同时也可识别地貌单元的位置和边界,如TCI≈1可作为平原与山地之间的分界值,TCI>2可视为高海拔和极高海拔山区分布范围,同时TCI可识别出相近海拔高度下不同地貌单元的分布。在高程分区下TCI>2时为各山系（山群）震荡高程区起始处,可视为山峰密集分布的区域,且山麓处TCI曲线差异显著。
（3）新疆拥有除海成地貌外几乎所有地貌类型,依据地貌成因类型及作用性质与地形复杂度范围进行对应,结合TCI阈值分布可以在一定程度上对成因及作用类型进行辅助判读。地形复杂度能较好的体现不同外营力对地表留下的痕迹,一定程度上也可表征外营力对不同成因地貌类型的贡献度。
地形复杂度作为地学研究邻域描述地表起伏变化的重要参数,尚且未有统一且全面的定义和衡量指标,本文为地形复杂度的量化提出较为科学的计算过程,并以新疆为例进行分析和验证,TCI的主要分布范围在0~4之间,受篇幅所限没有考虑TCI>10以上数值是否可视为突变异常值,还需结合高程进一步判断其是否为“噪声”,以期在后续的研究中进一步优化。

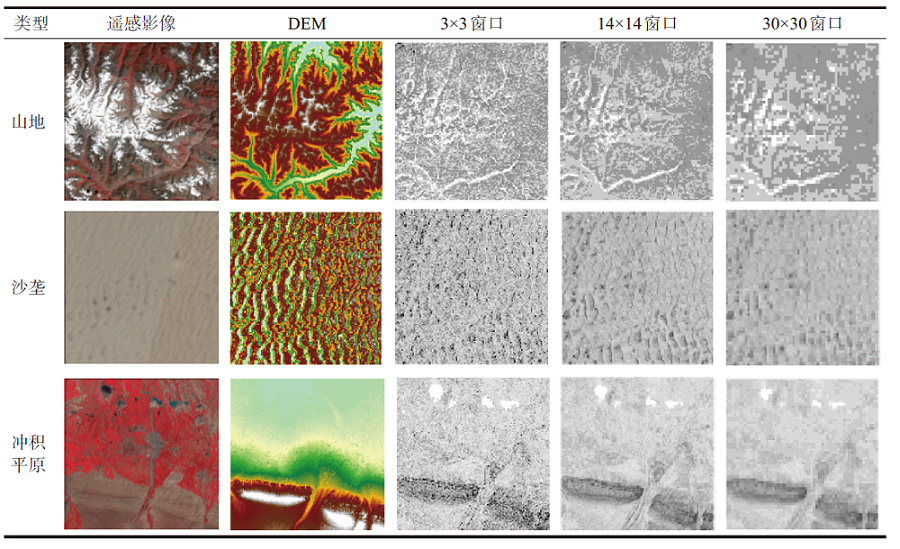真诚感谢匿名评审专家在论文评审中所付出的时间和精力,专家对本文引言部分语言表述、研究方法逻辑顺序及讨论部分升华等方面的修改意见,使本文获益匪浅。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
卢华兴, 刘学军, 汤国安. 地形复杂度的多因子综合评价方法. 山地学报, 2012, 30(5): 616-621.

[Lu Huaxing, Liu Xuejun, Tang Guoan. Terrain complexity assessment based on multivariate analysis. Journal of Mountain Science, 2012, 30(5): 616-621.] DOI: 10.16089/j.cnki.1008-2786.2012.05.011.

DOI

[2]
贾腾斌, 吴发启, 赵龙山, 等. 坡耕地上耕作形成的微地形复杂度特征与分析. 水土保持学报, 2013, 27(4): 152-156.

[Jia Tengbin, Wu Faqi, Zhao Longshan, et al. Micro-relief slope surface complexity characteristics of sloping farm land under different tillage practices. Journal of Soil and Water Conservation, 2013, 27(4): 152-156.] DOI: 10.13870/j.cnki.stbcxb.2013.04.039.

DOI

[3]
龙毅, 毋河海, 周侗, 等. 地图目标局部分形描述的元分维模型的实现. 武汉大学学报: 信息科学版, 2006, 31(10): 891-895.

[ [LongYi, Wu Hehai, Zhou Tong, et al. Implementation of meta fractal dimension model on localfractal description of map objects. Geomatics and Information Science of Wunan University, 2006, 31(10): 891-895.] DOI: 10.3969/j.issn.1671-8860.2006.10.012.

DOI

[4]
周侗.DEM元分维模型的构建方法与应用研究. 南京: 南京师范大学硕士学位论文, 2007: 9, 15.

[Zhou Tong.A dissertation submitted in partial fulfillment of the requirements for the degree of master of science. Nanjing: Master Dissertation of Nanjing Normal University, 2007: 9, 15.]

[5]
李天文, 刘学军, 汤国安. 地形复杂度对坡度坡向的影响. 山地学报, 2004, 22(3): 272-277.

[Li Tianwen, Liu Xuejun, Tang Guoan. Influence of terrain complexity on slope and aspect. Journal of Mountain Science, 2004, 22(3): 272-277.] DOI: 10.3969/j.issn.1008-2786.2004.03.003.

DOI

[6]
韩羽, 赵牡丹, 安巧绒, 等. DEM地形复杂度对坡度提取的影响分析. 陕西师范大学学报: 自然科学版, 2008, 36(S2): 78-79.

[Han Yu, Zhao Mudan, An Qiaorong, et al. Effect of terrain complexity on deriving slope from dem. Journal of Shaanxi Normal University: Natural Science Edition, 2008, 36(S2): 78-79.] DOI: 10.15983/j.cnki.jsnu.2008.s2.047.

DOI

[7]
何文秀, 石云. 黄土丘陵沟壑区地形复杂度分析. 测绘科学, 2015, 40(10): 146-152.

[He Wenxiu, Shi Yun. Analysis of terrain complexity in the hilly and gully area of loess plateau. Science of Surveying and Mapping, 2015, 40(10): 146-152.] DOI: 10.16251/j.cnki.1009-2307.2015.10.030.

DOI

[8]
Huaxing L U. Modelling Terrain Complexity. Berlin: Springer Berlin Heidelberg, 2008: 159-176.

[9]
Wilding T A, Palmer E, Polunin N. Comparison of three methods for quantifying topographic complexity on rocky shores. Marine Environmental Research, 2010, 69(3): 143-151. DOI: 10.1016/j.marenvres.2009.09.005.

DOI PMID

[10]
Huang Faming, Yang Jianbo, Zhang Biao, et al. Regional terrain complexity assessment based on principal component analysis and geographic information system: A case of Jiangxi Province, China. International Journal of Geo-Information, 2020, 9(9): 539. DOI: 10.3390/ijgi9090539.

DOI

[11]
韦玲霞. 基于地形复杂度的农用地整治项目选址适宜性评价: 以甘肃省天水市为例. 中国农业资源与区划, 2020, 41(1): 250-258.

[Wei Lingxia. Site selection suitability evaluation of agricultural land consolidation project based on the terrain complexity: Taking Tianshui City in Gansu Province as an example. Chinese Journal of Agricultural Resources and Regional Planning, 2020, 41(1): 250-258.] DOI: 10.7621/cjarrp.1005-9121.20200131.

DOI

[12]
刘进来, 马树恩, 刘玲. 基于GIS的露天开采矿区地形特征及植被恢复研究. 中国水土保持, 2016, (12): 62-66.

[Liu Jinglai, Ma Shuen, Liulin. Topography characteristics and vegetation restoration of open pit mining area based on GIS. Soil and Water Conservation in China, 2016, (12): 62-66.] DOI: 10.3969/j.issn.1000-0941.2016.12.024.

DOI

[13]
牛叔文, 秦静, 孙红杰, 等. 地形约束下的西部山区农业生产用地可持续利用评价: 以甘肃南部山区26县为例. 资源科学, 2010, 32(1): 50-56.

[Niu Shuwen, Qin Jing, Sun Hongjie, et al. An evaluation of sustainable development of agricultural production land based on terrain constraints in mountain areas of Western China: A case study of the southern mountain region of Gansu Province. Resources Science, 2010, 32(1): 50-56.] DOI: CNKI:SUN:ZRZY.0.2010-01-009.

DOI

[14]
牛叔文, 李景满, 李升红, 等. 基于地形复杂度的建设用地适宜性评价: 以甘肃省天水市为例. 资源科学, 2014, 36(10): 2092-2102.

[Niu Shuwen, Li Jingman, Li Shenghong, et al. Suitability assessment of construction land based on terrain complexity in Tianshui City. Resources Science, 2014, 36(10): 2092-2102.] DOI: CNKI:SUN:ZRZY.0.2014-10-012.

DOI

[15]
Ha T, Choi J Y, Yoo J, et al. Transformation of small-scale meteorological tsunami due to terrain complexity on the western coast of Korea. Journal of Coastal Research, 2014, 70(SP1): 284-289. DOI: 10.2112/SI70-048.1.

DOI

[16]
Park S Y, Lee H W, Lee S H, et al. Impact of the variation of sea breeze penetration due to terrain complexity on PBL development. Atmosphere, 2011, 20(2): 275-289. DOI: 10.5322/JES.2011.20.2.275.

DOI

[17]
Wang Kaicun, Zhou Xiuji, Liu Jingmiao, et al. Estimating surface solar radiation over complex terrain using moderate-resolution satellite sensor data. International Journal of Remote Sensing, 2005, 26(1): 47-58. DOI: 10.1080/01431160410001735111.

DOI

[18]
封志明, 李文君, 李鹏, 等. 青藏高原地形起伏度及其地理意义. 地理学报, 2020, 75(7): 1359-1372.

DOI

[Feng Zhiming, Li Wenjun, Li Peng, et al. Relief degree of land surface and its geographical meanings in the Qinghai-Tibet Plateau, China. Acta Geographica Sinica, 2020, 75(7): 1359-1372.] DOI: 10.11821/dlxb202007003.

DOI

[19]
江岭, 刘学军, 汤国安, 等. 地形分析中坡度坡向算法并行化方法研究. 计算机工程与科学, 2013, 35(4): 18-23.

[Jiang Ling, Liu Xuejun, Tang Guoan, et al. Parallel slope and aspect algorithm in terrain analysis. Computer Engineering and Science, 2013, 35(4): 18-23.] DOI: 10.3969/j.issn.1007-130X.2013.04.004.

DOI

[20]
王婷, 潘军, 蒋立军, 等. 基于DEM的地形因子分析与岩性分类. 国土资源遥感, 2018, 30(2): 231-237.

[Wang Ting, Pan jun, Jiang Lijun, et al. Topographic variable analysis and lithologic classification based on DEM. Remote Sensing for Land & Resources, 2018, 30(2): 231-237.] DOI: 10.6046/gtzyyg.2018.02.31.

DOI

[21]
汤国安, 李发源, 刘学军. 数字高程建模教程. 北京: 科学出版社, 2010: 141-142.

Tang Guoan, Li Fayuan, Liu Xuejun, et al. Digital Elevation Model. Beijing: Science Press, 2010: 141-142.]

[22]
汤国安, 赵牡丹, 李天文, 等. DEM提取黄土高原地面坡度的不确定性. 地理学报, 2003, 58(6): 824-830.

[Tang Guoan, Zhao Mudan, Li Tianwen, et al. Modeling slope uncertainty derived from DEMs in Loess Plateau. Acta Geographica Sinica, 2003, 58(6): 824-830.] DOI: 10.3321/j.issn: 0375-5444.2003.06.004.

DOI

[23]
刘春, 孙伟伟, 吴杭彬. DEM地形复杂因子的确定及与地形描述精度的关系. 武汉大学学报: 信息科学版, 2009, 34(9): 1014-1020.

[Liu Chun, Sun Weiwei, Wu Hangbin. Terrain complexity factor and its relationship with accuracy of DEM terrain representation. Geomatics and Information Science of Wunan University, 2009, 34(9): 1014-1020.] DOI: 10.13203/j.whugis2009.09.027.

DOI

[24]
刘滔.基于改进分形算法的地形复杂度模型构建及应用. 成都: 成都理工大学硕士学位论文, 2020: 10-12.

[Liu Tao.Construction and application of terrain complexity model based on improved fractal algorithm. Chengdu: Master Dissertation of Chengdu University of Technology, 2020: 10-12.]

[25]
邱炳文. 福建省龙海市土地利用空间分布影响因子的尺度效应分析. 自然资源学报, 2007, 22(1): 9.

[Qiu Bingwen. Scale effect analysis of driving forces of land-use patterns in Longhai City of Fujian Province. Journal of Natural Resources, 2007, 22(1): 9.] DOI: 10.3321/j.issn: 1000-3037.2007.01.009.

DOI

[26]
王让虎, 张树文, 蒲罗曼, 等. 基于ASTER GDEM和均值变点分析的中国东北地形起伏度研究. 干旱区资源与环境, 2016, 30(6): 49-54.

[Wang Ranghu, Zhang Shuwen, Pu Luoman, et al. Analysis on the relief amplitude in Northeast China based on ASTER GDEM and mean change point method. Journal of Arid Land Resources and Environment, 2016, 30(6): 49-54.] DOI: 10.13448/j.cnki.jalre.2016.180.

DOI

[27]
王玲, 同小娟. 基于变点分析的地形起伏度研究. 地理与地理信息科学, 2007, 23(6): 65-67.

[Wang Ling, Tong Xiaojuan. Analysis on relief amplitude based on change point method. Geography and Geo-Information Science, 2007, 23(6): 65-67.] DOI: 10.3969/j.issn.1672-0504.2007.06.015.

DOI

[28]
陈学兄, 常庆瑞, 郭碧云, 等. 基于SRTM DEM数据的中国地形起伏度分析研究. 应用基础与工程科学学报, 2013, 21(4): 670-678.

[Chen Xuexiong, Chang Qingrui, Guo Biyun, et al. Analytical study of the relief amplitude in China based on SRTM DEM data. Journal of Basic Science and Engineering, 2013, 21(4): 670-678.] DOI: 10.3969/j.issn.1005-0930.2013.04.009.

DOI

[29]
刘育成, 赵廷宁. 基于变点分析法提取废弃采石场地形起伏度的方法. 水土保持研究, 2016, 23(3): 269-273.

[Liu Yucheng, Zhao Tingning. Method for extraction relief amplitude of abandoned quarry based on change point method. Research of Soil and Water Conservaion, 2016, 23(3): 269-273.] DOI: 10.13869/j.cnki.rswc.2016.03.046.

DOI

[30]
钟静, 卢涛. 中国西南地区地形起伏度的最佳分析尺度确定. 水土保持通报, 2018, 38(1): 175-181, 186.

[Zhong Jing, Lu Tao. Optimal statistical unit for relief amplitude in Southwestern China. Bulletin of Soil and Water Conservation, 2018, 38(1): 175-181, 186.] DOI: 10.13961/j.cnki.stbctb.2018.01.031.

DOI

[31]
周成虎, 程维明, 钱金凯, 等. 中国陆地1:100万数字地貌分类体系研究. 地球信息科学, 2009, 11(6): 707-724.

[Zhou Chenghu, Cheng Weiming, Qian Jinkai, el al. Research on the classification system of digital land geomorphology of 1:1,000,000 in China Journal Of Geo-Information Science, 2009, 11(6): 707-724.] DOI: 10.3969/j.issn.1560-8999.2009.06.006..

[32]
黄骁力, 丁浒, 那嘉明, 等. 地貌发育演化研究的空代时理论与方法. 地理学报, 2017, 72(1): 94-104.

DOI

[Huang Xiaoli, Ding Hu, Na Jiaming, et al. Theories and methods of space-for-time substitution in geomorphology. Acta Geographica Sinica, 2017, 72(1): 94-104.] DOI: 10.11821/dlxb201701008.

DOI

[33]
程维明, 柴慧霞, 周成虎, 等. 新疆地貌空间分布格局分析. 地理研究, 2009, 28(5): 1157-1169.

[Cheng Weiming, Chai Huixia, Zhou Chenghu, et al. The spatial distribution patterns of digital geomorphology in Xinjiang. Geographical Research, 2009, 28(5): 1157-1169.] DOI: 10.3321/j.issn: 1000-0585.2009.05.002.

DOI

[34]
蒋广鑫, 谢元礼, 高志远, 等. 中国5类典型区域常用DEM高程精度评价. 水土保持研究, 2020, 27(5): 72-80.

[Jiang Guangxin, Xie Yuanli, Gao Zhiyuan, et al. Evaluation on elevation accuracy of commonly used dem in five typical areas of China. Research of Soil and Water Conservation, 2020, 27(5): 72-80.] DOI: 10.13869/j.cnki.rswc.2020.05.011.

DOI

[35]
周成虎, 程维明. 中国西部1:100万数字地貌数据集. 北京: 国家青藏高原科学数据中心,2019, CSTR: 18406.11.Geogra.tpdc.270104.

[Zhou Chenghu, 1:1000000 geomorphological map of Western China. Beijing: National Tibetan Plateau Data Center,2019, CSTR: 18406.11.Geogra.tpdc.270104.

[36]
张磊.基于核心地形因子分析的黄土地貌形态空间格局研究. 南京: 南京师范大学硕士学位论文, 2013: 15-16.

[Zhang Lei. Study on spatial pattern of loess landform based on core topographic factor analysis. Nanjing: Master Dissertation of Nanjing Normal University, 2013: 15-16.]

[37]
唐钰涵.一种基于局部地形复杂度指标的机载LiDAR地面点云数据抽稀方法. 成都: 西南交通大学硕士学位论文, 2019: 8-10.

[Tang Yuhan.A thin-method besed on local terrain complexity index for LiDAR bare earth surface point cloud. Chengdu: Master Dissertation of Southwest Jiaotong University, 2019: 8-10.]

[38]
薛玫娇.基于DEM的黄土丘陵沟壑区地形复杂度测算. 西安: 西安科技大学硕士学位论文, 2018: 13-19.

Xue Meijiao.Measure of terrain complexity in the hilly and gully area of loess plateau Based on DEM. Xi'an: Master Dissertation of Xi'an University of Science and Technology, 2018: 13-19.]

[39]
Wilson T H. Some distinctions between self-similar and self-affine estimates of fractal dimension with case history. Mathematical Geology, 2000, 32(3): 319-335. DOI: 10.1023/A: 1007585811281.

DOI

[40]
Florinsky I. Accuracy of local topographic variables derived from digital elevation models. International Journal of Geographical Information Systems, 1998, 12(1): 47-62. DOI: 10.1080/136588198242003.

DOI

[41]
周启鸣, 刘学军. 数字地形分析. 北京: 科学出版社, 2006: 210-263.

[Zhou Qiming, Liu Xuejun. Digital Topographic Analysis. Beijing: Science Press, 2006: 210-263.]

[42]
郝振纯, 安贵阳, 王加虎, 等. 不同地形下DEM的坡度坡向算法比较. 水电能源科学, 2011, 29(6): 68-70, 102.

[Hao Zhengchun, An Guiyang, Wang Jiahu, el at. Comparison of algorithms for calculating slope and exposure with different terrain based on DEM. Water Resources and Power, 2011, 29(6): 68-70, 102.] DOI: 10.3969/j.issn.1000-7709.2011.06.022.

DOI

[43]
谢轶群, 汤国安, 江岭. DEM提取坡向变率中的误差特征与消除方法. 地理与地理信息科学, 2013, 29(2): 53-57.

[Xie Yiqun, Tang Guoan, Jiang Ling. Characteristics and correcting methods of errors in extraction of SOA based on DEMS. Geography and Geo-Information Science, 2013, 29(2): 53-57.] DOI: 10.7702/dlydlxxkx20130211.

DOI

[44]
孔亚平, 张科利, 曹龙熹. 土壤侵蚀研究中的坡长因子评价问题. 水土保持研究, 2008, 15(4): 43-47, 52.

[Kong Yaping, Zhang Keli, Cao Longxi. Appraise slope length factors in soil erosion study. Research of Soil and Water Conservation, 2008, 15(4): 43-47, 52.] DOI: CNKI:SUN:STBY.0.2008-04-010.

DOI

[45]
喻红, 曾辉, 江子瀛. 快速城市化地区景观组分在地形梯度上的分布特征研究. 地理科学, 2001, 21(1): 64-69.

[Yu Hong, Zeng Hui, Jiang Ziying. Study on distribution characteristics of landscape elements along the terrain gradient. Scientia Geographica Sinica, 2001, 21(1): 64-69.] DOI: 10.3969/j.issn.1000-0690.2001.01.012.

DOI

[46]
韩海辉, 高婷, 易欢, 等. 基于变点分析法提取地势起伏度: 以青藏高原为例. 地理科学, 2012, 32(1): 101-10.

DOI

[Han Haihui, Gao Ting, Yi Huan, et al. Extraction of relief amplitude based on change point method: A case study on the Tibetan Plateau. Scientia Geographica Sinica, 2012, 32(1): 101-10.] DOI: 10.13249/j.cnki.sgs.2012.01.013.

DOI

[47]
张婷, 汤国安, 王春, 等. 黄土高原地形因子间关联性的神经网络分析. 地球信息科学, 2004, 6(4): 45-50.

[Zhang Ting, Tang Guoan, Wang Chun, el al. The relevancy between quantitative terrain factors and mean slope in China's Loess Plateau. Geo-Information Science, 2004, 6(4): 45-50.] DOI: 10.3969/j.issn.1560-8999.2004.04.011.

DOI

[48]
张倩宁, 黄泽纯, 徐柱, 等. 一种自适应定权地形复杂度模型. 山地学报, 2017, 35(2): 230-237.

[Zhang Qianning, Huang Zechun, Xu Zhu, et al. An adaptive weighting terrain complexity model. Journal of Mountain Science. 2017, 35(2): 230-237.] DOI: 10.16089/j.cnki.1008-2786.000216.

DOI

[49]
张鹏.基于主成分分析的综合评价研究. 南京: 南京理工大学硕士学位论文, 2004: 28-38.

[Zhang Peng.Comprehensive evaluation research based on principal component analysis. Nanjing: Master Dissertation of Nanjing University of Science and Technology, 2004: 28-38.]

[50]
汤良杰, 邱海峻, 云露, 等. 塔里木盆地北缘-南天山造山带盆-山耦合和构造转换. 地学前缘, 2012, 19(5): 10.

[Tang Liangjie, Qiu Haijun, Yun Lu, et al. Analysis of basin-mountain coupling and transition of the Northern Tarim Basin-Southern Tianshan Orogenic Belt. Earth Science Frontiers, 2012, 19(5): 10.] DOI: CNKI:SUN:DXQY.0.2012-05-021.

DOI

[51]
田瑞云, 王玉宽, 傅斌, 等. 基于DEM的地形单元多样性指数及其算法. 地理科学进展, 2013, 32(1): 122-130.

[Tian Ruiyun, Wang Yukuan, Fu Bin, et al. DEM-based topographic unit diversity index and its algorithm. Progress in Geography, 2013, 32(1): 122-130.] DOI: 10.3724/SP.J.1033.2013.00121.

DOI

[52]
赵洪壮, 李有利, 杨景春, 等. 天山北麓河流纵剖面与基岩侵蚀模型特征分析. 地理学报, 2009, 64(5): 563-570.

[Zhao Hongzhuang, Li Youli, Yang Jingchun, et al. The longitudinal profiles of the ten rivers in North Tianhan Mountains and their tectonic significance. Acta Geographica Sinica, 2009, 64(5): 563-570.] DOI: 10.3321/j.issn: 0375-5444.2009.05.005.

DOI

[53]
杨景春, 李有利. 地貌学原理(修订版). 北京:北京大学出版社, 2005:26.

Yang Jingchun, Li Youli. Geomorphological Principles. Beijing: Beijing University Press, 2005: 26.]

[54]
柴慧霞, 周成虎, 陈曦, 等. 基于地理格网的新疆地貌区划方法与实现. 地理研究, 2008, 27(3): 481-492, 725-726.

[Chai Huixia, Zhou Chenghu, Chen Xi, et al. The new methodology of geomorphologic zonalization in Xinjiang based on geographical grid. Geographical Research, 2008, 27(3): 481-492, 725-726.] DOI: 10.3321/j.issn: 1000-0585.2008.03.001

DOI

[55]
程维明, 赵尚民. 中国冰川地貌空间分布格局研究. 冰川冻土, 2009, 31(4): 587-596.

[Cheng Weiming, Zhao Shangmin. Study of the spatial distribution pattern of the digital glacial geomorphology in China. Journal of Glaciology and Geocryology, 2009, 31(4): 587-596.] DOI: CNKI:SUN:BCDT.0.2009-04-000.

DOI

[56]
周成虎, 程维明, 钱金凯. 数字地貌遥感解析与制图. 北京: 科学出版社, 2009: 11.

[Zhou Chenghu, Chen Weiming, Qian Jinkai. Remote Sensing Analysis and Mapping of Digital Landforms. Beijing: Science Press, 2009: 11.]

Options
文章导航

/

〈 〉